Tree ( Pohon )

 TREE adalah suatu graph yang acyclic, simple, connected yang tidak mengandung loop.

General TREE

ROOT Tree A ; suatu vertex dengan derajat masuk = 0.

LEAF Tree A ; suatu vertex dengan derajat keluar = 0.

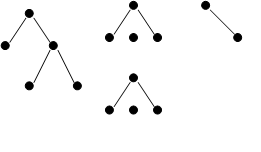
Tree A atas vertex-vertex : V1, V2, V3, ....... , Vn harus mempunyai :

1.   Satu root A         Root (A) =  V1

2.   Sisanya (V2 , V3, ........,Vn) dipartisi menjadi Tm subtree ; di mana : 0 m n-1

Contoh :    TREE A

Keterangan :

    Root (A) = B

    Leaf (A) = A,C,D,G,H

    B mempunyai 4 subtree : A,C,I,D

    I mempunyai 2 subtree : E,F

    E mempunyai 1 subtree : G

    F mempunyai 1 subtree : H

LEVEL dari suatu vertex A dalam Tree A adalah LENGTH Path(P) (Root(A),A)

Dari gambar Tree A ;

         - Tentukan level A :

                Length P(Root(A),A)

                Length P(B,A) = (B,A) = 1

         - Tentukan level G :

                Length P(Root(A),G)

                Length P(B,G) = (B,I) (I,E) (E,G) = 3

HIGH dari suatu tree A adalah level tertinggi ditambah 1.

WEIGHT dari suatu tree A adalah jumlah leaf dalam tree A.

Contoh :    Dari Tree A ;   High Tree A = 3 + 1 = 4

                                          Weight Tree A = 5 (A,C,D,G,H)

FOREST

Forest merupakan koleksi dari tree-tree.

      Contoh :   

BINARY TREE

     

Binary Tree merupakan himpunan vertex-vertex yang terdiri dari 2 subtree (dengan disjoint) yaitu subtree kiri dan subtree kanan.

      Setiap vertex dalam binary tree mempunyai derajat keluar max = 2.

      Contoh :

                  (1)                             (2)                              (3)

         

      Derajat keluar = 2             A adalah subtree kanan          A adalah subtree kiri

                  (4)                                                    (5)

               

                 

      Bukan Binary Tree tapi                             Bukan Binary Tree tapi General Tree

     General Tree karena bukan                       karena mempunyai derajat keluar > 2.

      merupakan Subtree Kiri/Kanan

SIMILAR & EKIVALEN dalam 2 BINARY TREE

         

Dua Binary Tree dikatakan Similar, jika struktur dari kedua Binary Tree sama.

Contoh :

                            T1                                               T2

                 

Dua Binary Tree dikatakan Ekivalen, jika :

            - Similar

            - Informasi setiap vertex sama.

Contoh :

                              T3                                             T1

                 
         

COMPLETE

Mis. height dari binary tree T adalah k.

Binary Tree T disebut COMPLETE jika jumlah verteks dari binary tree T adalah:

            k-1

        2 i             (mencapai maximum)

            i = 0

Contoh height dari binary tree T = 4. Gambar binary tree-nya :

            4-1

         2 i = (20 + 21 + 22 + 23) = 15 vertex                          

            i = 0

            

ALMOST  COMPLETE

Mis. height dari binary tree T adalah k.

Binary Tree T disebut ALMOST COMPLETE  jika :

- pada level 0 hingga level k - 2, jumlah verteksnya adalah:

                                    k-1

                               2 i

                                    i = 0

   - pada level k - 1 verteks-verteksnya terisi dari kiri ke kanan sebagai u,
     dimana 1 <= u <= 2 k-1

Contoh height dari binary tree T = 4. dan mis u = 5.

Gambar binary tree-nya :

            4-2

        2 i = (20 + 21 + 22 ) = 7                                    

            i = 0

HEIGHT MIN dan HEIGHT MAX

H min = [ log 2 (N+1) ]                       H max = N

           = Fungsi celling dengan pembulatan ke atas

N       = jumlah vertex

Contoh :

Diberi 7 buah vertex untuk membentuk suatu binary tree.

Hitung H min dan H max dari kemungkinan binary tree yang terbentuk.

Gambar binary treenya.

Jawab : H min = [ log 2 (7+1) ]                   H max = N = 7

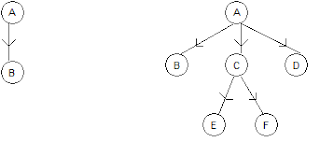
REPRESENTASI BINARY TREE

Contoh :

Algoritma untuk merubah General Tree menjadi Binary tree:

1.Insert edge-edge yang menghubungkan sibling (saudara) kemudian      delete semua edge yang menghubungkan parent dengan child-nya kecuali edge yang paling kiri.

2.Rotasi  45o sedemikian sehingga dibedakan subtree kiri dan kanan.

Contoh :

                                               (1)                                         (2)

 
                                                          (3)

Algoritma untuk merubah Forest menjadi Binary tree:

1. Insert edge-edge yang menghubungkan sibling (saudara) kemudian     delete semua edge yang menghubungkan parent dengan child-nya kecuali edge yang paling kiri.

2. Tree-tree yang lain dihitung sebagai satu level

Contoh :

                                            (1)                       (2)       (3)       (4)       (5)           

BINARY TREE TRANSVERSAL

Adalah proses menelusuri suatu Binary Tree sehingga sedemikian rupa setiap vertex dikunjungi hanya 1 kali.

3 aktivitas dalam Binary tree Transversal :

(1)       Visit the Root

(2)       Transverse the left subtree

(3)       Transverse the right subtree

Algoritma dalam Binary Tree Transversal :

1.         PRE-ORDER TRANSVERSAL

            a.         visit the root

            b.         tranverse the left subtree

            c.         tranverse the right subtree

2.         IN-ORDER TRANSVERSAL

            a.         tranverse the left subtree

            b.         visit the root

            c.         tranverse the right subtree

3.         POST-ORDER TRANSVERSAL

            a.         tranverse the left subtree

            b.         tranverse the right subtree

            c.         visit the root

BINARY SEARCH TREE

           

- suatu Binary Search Tree dari himpunan N record (N1, N2, N3 . . . Nn)

- adalah suatu Binary Tree yang setiap vertex-nya (sebut Ri) ditempati oleh Ni untuk i = 1,2,3 ... N.

Vertex-vertex dari Binary Tree tsb. diatur sedemikian rupa sehingga untuk setiap Ri harus memenuhi syarat sbb :

1.         Jika Rj = left (Ri) maka Nj < Ni

2.         Jika Rj = right (Ri) maka Nj > Ni

Contoh :

Diketahui key dari 7 record (K, M, L, N, P, O, Q)

Binary Search Tree dari 7 key diatas dapat dibentuk :

           

Operasi-operasi pada Binary Search Tree : 
1.         Direct Search 

2.         Sequential Search 

3.         Insert Search 

4.         Delete Search

ad.1. DIRECT SEARCH

untuk mencari vertex k dalam binary search tree dengan root=Ri ,

algoritmanya adalah sbb :

1. Jika tree kosong maka search tidak sukses

    (k tidak ada dalam binary search tree)

2. Jika k = Ni maka search sukses

    (k ada dalam binary search tree)

3. Jika k < Ni maka subtree kiri dari Ri ditelusuri dan Ri = left    

    (Ri) kemudia         kembali ke langkah 1.

4. jika k > Ni maka subtree kanan dari Ri ditelusuri dan Ri=right

    (Ri) kembali ke langkah 1.

Contoh :

Carilah Key M dalam Binary Tree berikut secara Direct Search.

Berapa langkah/perbandingan yang dibutuhkan untuk mencari Key M.

Bandingkan dengan rootnya, jika :

            - lebih besar maka cari ke kanan

            - lebih kecil maka cari ke kiri.

N, K, M           -- 3 kali perbandingan

M : N               -- M < N

     M : K               -- M > K

     M : M  

ad.2.   SEQUENTIAL SEARCH

untuk mencari vertex K dalam binary search tree dengan Root=Ri.

Algoritmanya menggunakan langkah-langkah : IN-ORDER Transversal (Left Visit Right)

Contoh :

Cari key M dalam Binary Tree berikut secara sequential.

ad.3.   INSERT SEARCH

            Prinsipnya sama dengan DIRECT.

            4 langkah :    K > A 

                                  F > A

                                       D > A

                                       A = A

ad. 4.  DELETE SEARCH

            dilihat dari  Link -list-nya.

BALANCED TREE

           

Suatu Binary Tree dimana untuk setiap Root Ri berlaku struktur subtree kiri = struktur subtree kanan.

Contoh :

HEIGHT BALANCED TREE

Suatu Tree dimana untuk setiap Root Ri berlaku height dari subtree kanan dan height dari subtree kiri beda paling banyak satu.

Contoh :

                                  Height balanced Tree                                 Bukan

                                             1                    2               3

Height Balanced tree belum tentu Balance Tree tapi Balance Tree sudah pasti height balance tree.

Binary tree yang Complete = Balance Tree

Balance Tree belum tentu Binary Tree Complete :

Height Balance Tree belum tentu Binary Tree Complete :

Height Balance Tree belum tentu Almost Complete :

                                                        Balance + Almost        

Balance Tree = Almost Complete :

                                              almost + balance      almost + balance